背景:说到并行计算,我想对很多人来说早就如雷贯耳了,并行计算目前有两个比较主流的应用手段:MPI , OpenMP (或者 二者配合)。很多人都“歧视”openmp,推崇MPI,认为openmp只不过是几个编译指令而已,很容易掌握,看起来没有MPI复杂,但是我可以说MPI也只不过是一堆消息传递函数而已吗,我个人认为MPI的主要难度在于对原始算法的修改,因为它一般需要一些数理基础。而OpenMP相对更加容易应用,而且实际上一般情况下,只能用OpenMP,这是因为:(1)MPI适用于“分布式多计算机”,也就是由多个计算机连结的工作站集群,我们所(青藏高原研究所)虽然有阳坤老师的一个由10个计算节点组成的工作站,但是由于我只是“下等”用户,每次最多只会分配给我一个节点,申请的节点多于一个就要无限期排队,这个先决条件就迫使我放弃MPI;(2)OpenMP适用于“集中式多处理器”,一台多核笔记本就完全满足条件了,而且,OpenMP的技术规范内容比较简单,易于掌握,可以实现快速应用,这对于我们这些“急于毕业”的人来说尤为重要。
然后,考虑实际问题:要对模型进行并行化,实际上就是对组成模型的各个函数进行修改,但是物理机制的模型通常是比较复杂的,函数很多,所以首先要搞清楚哪些函数是“真正重要”的,是值得修改的,下面是我做的统计:
——————————————————————————————-
for (y = 0; y < Map->NY; y++) {
。。。
。。。
}
}
先测一下两块儿的时间(标红的是重点):
pre-openmp time for main_gl is: 1 ms
1st loop for main_gl is: 114 ms
Glacier Model not run (Static Option)
2nd loop for main_gl is: 110 ms
Domain glacier-covered area = 19.892 percent
Snow-covered area = 61.939 percent
Watershed Snow-covered area = 61.939 percent
Watershed glacier-covered area = 19.892 percent
ALL DONE: 0.08 yr integration
uncertain time for main_gl is: 34 ms
可以看到,循环前耗时1ms,循环后耗时34ms(我称它为uncertain是因为这部分代码在做IO),两个循环分别耗时114和110毫秒。
好了,我们要实施并行计算了,在这里加上OpenMP编译指令,即:
#pragma omp parallel for num_threads(4) schedule(static, chunk_size) reduction(+: count, n_mask)
其中,chunk_size是简单的=总栅格数 / cpu核数,此外,要注意好线程私有、共享变量等细节,另一个块的指令是类似的。另外,我指定的核数是4核,这是为了尽量使运行时的各个线程可以在高频下运行。
然后,再次编译运行模型,只让模型运行一个时间步,得到这两块循环的运行时间:
1st loop for main_gl is: 35 ms
Glacier Model not run (Static Option)
2nd loop for main_gl is: 22 ms
果然,114对比35,110对比22,目测速度快了很多,兴奋之余,问题来了:我指定的是4核,前者的速度只提高了3倍有余,而后者提高了近5倍,这是在逗我吗 ,即便是考虑到线程切换的额外消耗,这个对比也太异常了一点。
,即便是考虑到线程切换的额外消耗,这个对比也太异常了一点。
先来说下为什么单核变4核会使第二个循环提升5倍速度,原因很可能与每个核的独立cache有关,我单核运行的时候只会用到一个核的cache,而四核运行时则会充分利用各个核的1、2级缓存,大大提高了高速缓存的使用量,而且第二个循环处理了两个大数组,这两个大数组的体积早就超过了单个核的2级缓存,所以这里进行并行不仅有了多线程的优势,还附带有高速缓存的加速。
但是,对于第一个循环,为什么只提高了3倍的速度呢,首先要解决这个疑问,从头审视一下模型源码就会发现,问题在于负载不均衡:该模型遍历的是一个矩形区域,而参与计算的只是其中被标记的流域栅格,所以,如果我只是简单的四等分,显然会造成有的区域mask栅格多,有的区域较少的情况,而并行运算的时间是由“负载”最重的那个线程决定的,so,在大多数实际情况下,我这样应用的效率是较低的。看起来,我似乎找到答案了。
那么,为了能够继续进行下去,我觉得有必要实现一个函数工具包,用于自动划分子任务,well,KB的一周就从这一刻开始了——
我首先定义了一个用于评定划分效果的“判断标准” —— load_balance = 最小负载 / 最大负载,这个值越大,则认为划分越有效,效果越好。(恩,这个很容易理解)
最容易想到的划分方式当然是按行来划分,即水平划分,但是,很多情况下,栅格之间是会相互影响的,尤其是在水文模型中,相邻的栅格之间会有“流入”、“流出”这类影响,所以直接划分会导致计算错误,所以,我引入了intervals的概念,而且为了真正实现负载均衡,还需要加入“权重”的设置,我的简单实现如下:
/*
* Params:
* task_mask: the task to be extracted from
* flag_values: may be an array containing flags indicating time-expensive
* flag_weights: an array paired with flag_values indicating the weight of
* corresponding flag_value
* flag_num: num of flag_values
* cols: num of cloumns for task
* rows: num of rows for task
* interval: num of lines between each adjacent subtask
* num_subtasks: num of sub tasks to be divided into
*
* Returns: line index(0-based) where the new subtask ends
*
* Note: this func is not to extract all subtasks all at once,
* but to extract one subtask for a call
* */
int
extract_subtask_by_line(int **task_mask, int cols, int rows, int num_subtasks,
int *flag_values, float *flag_weights, int flag_num)
{
int ns = num_subtasks;
if (ns == 1) {
return cols * rows -1;
}
if (ns <= 0) {
fprintf(stderr, “Error: num of subtasks %d <= 0\n”, ns);
exit(1);
}
float total = load_value(task_mask, cols, rows, flag_values,
flag_weights, flag_num);
int i = 0;
float sum = 0.f;
for (i=0; i<rows; i++) {
int **task_line = &task_mask[i];
sum += load_value(task_line, cols, 1, flag_values,
flag_weights, flag_num);
if (sum >= total / num_subtasks) {
#if DBG_SUBTASK
printf(“Load value : %f, when remaining %d subtasks.\n”,
sum, num_subtasks);
if (num_subtasks == 2) {
sum = total – sum;
printf(“Load value : %f, for the last subtask.\n”,
sum);
}
#endif
return i;
}
}
return -1;
}
/*
* Description:
* Horizontally, average all lines into `num_subtasks’ subtasks,
* based on flag weightings.
*
* Returns: 1 for success, otherwise 0
*/
int
extract_subtasks_by_line(int **task_mask, int cols, int rows, int num_subtasks,
int *flag_values, float *flag_weights, int flag_num,
int *endline_labels)
{
int nr = rows;
int ns = num_subtasks;
int i = 0;
int forward = 0;
int line = 0;
for (; i<num_subtasks-1; ++i) {
#if DBG_SUBTASK
printf(“Extracting %dth subtask, forwarding %dth(0-based) line\n”, i, forward);
#endif
line = extract_subtask_by_line(task_mask+forward,
cols, nr, ns, flag_values, flag_weights, flag_num);
if (line < 0) {
fprintf(stderr, “Error: failed to extract %dth subtask\n”, i);
return 0;
}
forward += line + 1;
endline_labels[i] = forward;
nr -= line + 1;
–ns;
}
endline_labels[num_subtasks-1] = rows – 1;
return 1;
}
/*
* Description: this func inserts needed intervals and updates
* original subtasks’ endline_labels
*/
int
insert_interval_by_line(int interval, int **task_mask, int cols, int rows,
int num_subtasks, int *flag_values, float *flag_weights, int flag_num,
int *startline_labels, int *endline_labels)
{
int i = 0;
int sline0 = 0;
int sline1 = 0;
int eline0 = 0;
int eline1 = 0;
for (; i<num_subtasks-1; ++i) {
eline0 = endline_labels[i];
sline1 = eline0 + 1;
eline1 = endline_labels[i+1];
int k = 0;
for (; k<interval; k++) {
float load0 = load_value(&task_mask[sline0], cols, eline0 – sline0 + 1,
flag_values, flag_weights, flag_num);
float load1 = load_value(&task_mask[sline1], cols, eline1 – sline1 + 1,
flag_values, flag_weights, flag_num);
if (load0 >= load1) {
–eline0;
}
else {
++sline1;
}
}
if (eline0 < sline0 || eline1 < sline1) {
fprintf(stderr, “Error: startline exceeds endline, with %d-%d %d-%d, \
when inserting %dth interval\n”, sline0, eline0, sline1, eline1, k);
return 0;
}
startline_labels[i] = sline0;
startline_labels[i+1] = sline1;
endline_labels[i] = eline0;
endline_labels[i+1] = eline1;
sline0 = sline1;
}
#if DBG_SUBTASK
int dbg = 0;
for (; dbg<num_subtasks; ++dbg) {
printf(“After inserting intervals, \
the %dth subtask is from line %d to %d\n”,
dbg, startline_labels[dbg],endline_labels[dbg]);
}
#endif
return 1;
}
/*
* Returns: bool flag indicating whether dividing is successful
*/
int
horizontal_divide(int **task_mask, int cols, int rows, int num_subtasks, int interval,
int *flag_values, float *flag_weights, int flag_num,
int ***subtasks_x, int ***subtasks_y, int ***intervals_x, int ***intervals_y,
int **count_subtasks, int **count_intervals,
float *load_balance)
{
#if DBG_SUBTASK
printf(“Start doing horizontal dividing…\n”);
#endif
int endline_labels[num_subtasks];
int startline_labels[num_subtasks];
if (extract_subtasks_by_line(task_mask, cols, rows, num_subtasks,
flag_values, flag_weights, flag_num, endline_labels)
< 0) {
fprintf(stderr, “Error: failed to averagely divide horizontally, before \
inserting intervals.\n”);
return 0;
}
#if DBG_SUBTASK
printf(“All sub tasks have been divided out, without intervals\n”);
int sl[num_subtasks];
int el[num_subtasks];
int dbg0 = 0;
int dbg1 = 0;
for (; dbg0<num_subtasks; ++dbg0) {
sl[dbg0] = dbg1;
el[dbg0] = endline_labels[dbg0];
dbg1 = el[dbg0] + 1;
}
float lb0 = horizontal_divide_load_balance(task_mask, cols, num_subtasks,
flag_values, flag_weights, flag_num,
sl, el);
printf(“Load balance value is: %f, using horizontally dividing, \
before inserting inervals\n”, lb0);
#endif
*subtasks_y = (int **)calloc(num_subtasks, sizeof(int *));
*subtasks_x = (int **)calloc(num_subtasks, sizeof(int *));
if (interval > 0) {
*intervals_x = (int **)calloc(num_subtasks-1, sizeof(int *));
*intervals_y = (int **)calloc(num_subtasks-1, sizeof(int *));
}
else {
*intervals_x = NULL;
*intervals_y = NULL;
}
if (!insert_interval_by_line(interval, task_mask, cols, rows,
num_subtasks, flag_values, flag_weights, flag_num,
startline_labels, endline_labels)) {
fprintf(stderr, “Error: failed to insert intervals, when doing horizontal divide.\n”);
return 0;
}
*load_balance = horizontal_divide_load_balance(task_mask, cols, num_subtasks,
flag_values, flag_weights, flag_num,
startline_labels, endline_labels);
#if DBG_SUBTASK
printf(“Load balance value is: %f, using horizontally dividing, \
after inserting intervals\n”, *load_balance);
#endif
int i = 0;
for (; i<num_subtasks-1; i++) {
if (startline_labels[i+1] – endline_labels[i] – 1 != interval) {
fprintf(stderr, “Error: the spacing lines between %dth and %dth subtask \
don’t match the interval %d, with endline- %d, startline- %d\n”, i, i+1, interval,
endline_labels[i], startline_labels[i+1]);
}
int *tmp = (int *)calloc((endline_labels[i]-startline_labels[i]+1)*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for subtasks_x[%d]\n”, i);
return 0;
}
(*subtasks_x)[i] = tmp;
tmp = NULL;
tmp = (int *)calloc((endline_labels[i]-startline_labels[i]+1)*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for subtasks_y[%d]\n”, i);
return 0;
}
(*subtasks_y)[i] = tmp;
if (interval > 0) {
tmp = NULL;
tmp = (int *)calloc(interval*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for intervals_x[%d]\n”, i);
return 0;
}
(*intervals_x)[i] = tmp;
tmp = NULL;
tmp = (int *)calloc(interval*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for intervals_y[%d]\n”, i);
return 0;
}
(*intervals_y)[i] = tmp;
}
tmp = NULL;
if (i == num_subtasks-2) {
tmp = (int *)calloc((endline_labels[i+1]-startline_labels[i+1]+1)*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for subtasks_x[%d]\n”, i+1);
return 0;
}
(*subtasks_x)[i+1] = tmp;
tmp = NULL;
tmp = (int *)calloc((endline_labels[i+1]-startline_labels[i+1]+1)*cols, sizeof(int));
if (tmp == NULL) {
fprintf(stderr, “Error: can’t calloc for subtasks_y[%d]\n”, i+1);
return 0;
}
(*subtasks_y)[i+1] = tmp;
tmp = NULL;
}
}
*count_subtasks = (int *)calloc(num_subtasks, sizeof(int));
*count_intervals = (int *)calloc(num_subtasks-1, sizeof(int));
int k = 0;
int j = 0;
for (i=0; i<num_subtasks-1; ++i) {
int count = 0;
for (j=startline_labels[i]; j<=endline_labels[i]; ++j) {
for (k=0; k<cols; ++k) {
(*subtasks_x)[i][count] = k;
(*subtasks_y)[i][count] = j;
++count;
}
}
(*count_subtasks)[i] = count;
count = 0;
for (j=endline_labels[i]+1; j<=endline_labels[i]+interval; ++j) {
for (k=0; k<cols; ++k) {
(*intervals_x)[i][count] = k;
(*intervals_y)[i][count] = j;
++count;
}
}
(*count_intervals)[i] = count;
if (i == num_subtasks – 2) {
count = 0;
for (j=startline_labels[i+1]; j<=endline_labels[i+1]; ++j) {
for (k=0; k<cols; ++k) {
(*subtasks_x)[i+1][count] = k;
(*subtasks_y)[i+1][count] = j;
++count;
}
}
(*count_subtasks)[i+1] = count;
}
}
return 1;
}
该实现分两步:首先不考虑子块之间的间隔,直接按照子块负载值进行平均分配,然后再在各个块的边界插入“隔离带”(intervals),插入的原则是:负载值相对较高的子块会被插入。(这里当然不够准确,只是为了简化实现)
要实施这个划分,就要清楚整个矩形区域的”负载分布“,所以,我统计了在第一个循环中,Mask栅格和非Mask栅格的总耗时,然后除以各自的总数,得到两者的耗时比例为3:1,那么我就可以定义flag_weights = {3, 1},把此权重带入“水平划分” ,得到的划分结果为:
Start doing horizontal dividing…
Extracting 0th subtask, forwarding 0th(0-based) line
Load value : 341289.000000, when remaining 4 subtasks.
Extracting 1th subtask, forwarding 257th(0-based) line
Load value : 339405.000000, when remaining 3 subtasks.
Extracting 2th subtask, forwarding 438th(0-based) line
Load value : 339485.000000, when remaining 2 subtasks.
Load value : 339159.000000, for the last subtask.
All sub tasks have been divided out, without intervals
Load value of 0th subtask is: 342926.000000
Load value of 1th subtask is: 339873.000000
Load value of 2th subtask is: 339335.000000
Load value of 3th subtask is: 337204.000000
Load balance value is: 0.983314, using horizontally dividing, before inserting inervals
负载均衡值达到了98%,看起来还不错,这里我没有加入“隔离带”,因为在这个循环里,各个栅格之间是互不影响的,下面看下实际运行效果。
1st loop for main_gl is: 28 ms
Glacier Model not run (Static Option)
2nd loop for main_gl is: 22 ms
耗时减少为28ms,114对比28,差不多刚好4倍,本来进行到这里就应该告一段落了,但是,有些人是有强迫症的,不折腾到一定程度是很难罢手的。
回过头来考虑划分方法,如果只是简单的“水平划分”,那么随着“核数”的增加,在存在“隔离带”的情况下,负载均衡值还会保持高水平吗?
这里做一个假设的情景:在计算河道汇流时,相邻栅格会有“依赖性”,所以这时需要加入“隔离带”,如果以行为单位的话,隔离带就应该是两行,我的研究区所覆盖的范围是:868行 x 807列,此外,我只计算被标记为流域的栅格。
那么,我调用“水平划分”,得到:
Start doing horizontal dividing…
Extracting 0th subtask, forwarding 0th(0-based) line
Load value : 82596.000000, when remaining 4 subtasks.
Extracting 1th subtask, forwarding 294th(0-based) line
Load value : 82315.000000, when remaining 3 subtasks.
Extracting 2th subtask, forwarding 440th(0-based) line
Load value : 82396.000000, when remaining 2 subtasks.
Load value : 82124.000000, for the last subtask.
All sub tasks have been divided out, without intervals
Load value of 0th subtask is: 83005.000000
Load value of 1th subtask is: 82554.000000
Load value of 2th subtask is: 82347.000000
Load value of 3th subtask is: 81525.000000
Load balance value is: 0.982170, using horizontally dividing, before inserting inervals
After inserting intervals, the 0th subtask is from line 0 to 292
After inserting intervals, the 1th subtask is from line 295 to 439
After inserting intervals, the 2th subtask is from line 442 to 576
After inserting intervals, the 3th subtask is from line 579 to 867
Load value of 0th subtask is: 82186.000000
Load value of 1th subtask is: 81906.000000
Load value of 2th subtask is: 81100.000000
Load value of 3th subtask is: 80927.000000
Load balance value is: 0.984681, using horizontally dividing, after inserting intervals
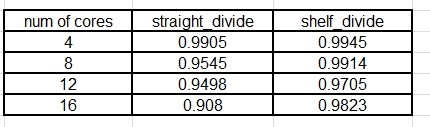
在4核的情况下,负载均衡可达到98.4%,随后,我又计算了8核、12核、16核的情况。
结果,
8核:Load balance value is: 0.954523, using horizontally dividing, after inserting intervals
12核:Load balance value is: 0.940436, using horizontally dividing, after inserting intervals
16核:Load balance value is: 0.906926, using horizontally dividing, after inserting intervals
性能下降还是比较明显的,那么索性就把我能想到的、比较容易实现的划分都做了吧,有水平,就自然想到了垂直划分:
int
vertical_divide(int **task_mask, int cols, int rows, int num_subtasks, int interval,
int *flag_values, float *flag_weights, int flag_num,
int ***subtasks_x, int ***subtasks_y, int ***intervals_x, int ***intervals_y,
int **count_subtasks, int **count_intervals,
float *load_balance)
{
/* create buffers to store data rotated horizontally */
#if DBG_SUBTASK
printf(“Start vertical dividing…\n”);
#endif
int hrows = cols;
int hcols = rows;
int **hdata = (int **)calloc(hrows, sizeof(int *));
if (hdata == NULL) {
fprintf(stderr, “Error: can’t calloc for hdata\n”);
exit(1);
}
int *hbuf = (int *)calloc(hcols*hrows, sizeof(int));
if (hbuf == NULL) {
fprintf(stderr, “Error: can’t calloc for hbuf\n”);
exit(1);
}
int i = 0;
for (; i<hrows; ++i) {
hdata[i] = hbuf + i*hcols;
}
/* convert vertical indexs and values to horizontal ones */
int j = 0;
for (i=0; i<hrows; ++i) {
for (j=0; j<hcols; ++j) {
hdata[i][j] = task_mask[j][i];
}
}
int **hsubtasks_x = NULL;
int **hsubtasks_y = NULL;
int **hintervals_x = NULL;
int **hintervals_y = NULL;
if (!horizontal_divide(hdata, hcols, hrows, num_subtasks, interval,
flag_values, flag_weights, flag_num,
&hsubtasks_x, &hsubtasks_y, &hintervals_x, &hintervals_y,
count_subtasks, count_intervals,
load_balance)) {
fprintf(stderr, “Error: failed to do horizontally dividing, \
before converting to vertical ones\n”);
return 0;
}
*subtasks_x = hsubtasks_x;
*subtasks_y = hsubtasks_y;
for (i=0; i<num_subtasks; ++i) {
int hncols = 0;
while (hsubtasks_y[i][hncols] == hsubtasks_y[i][0]) {
++hncols;
}
int hnrows = (*count_subtasks)[i] / hncols;
int ox = hsubtasks_y[i][0];
int oy = hsubtasks_x[i][0];
int nrows = hncols;
int ncols = hnrows;
int ci = 0;
int ri = 0;
int c = 0;
for (ri=0; ri<nrows; ++ri) {
for (ci=0; ci<ncols; ++ci) {
(*subtasks_x)[i][c] = ox + ci;
(*subtasks_y)[i][c] = oy + ri;
++c;
}
}
}
#if DBG_SUBTASK
int dbg = 0;
for (; dbg<num_subtasks; ++dbg) {
printf(“After vertical dividing, \
%dth subtask’s extent is from %d to %d in x dir, and from %d to %d in y dir\n”,
dbg, (*subtasks_x)[dbg][0], (*subtasks_x)[dbg][(*count_subtasks)[dbg]-1],
(*subtasks_y)[dbg][0], (*subtasks_y)[dbg][(*count_subtasks)[dbg]-1]);
}
#endif
if (interval > 0) {
*intervals_x = hintervals_x;
*intervals_y = hintervals_y;
for (i=0; i<num_subtasks-1; ++i) {
int hncols = 0;
while (hintervals_y[i][hncols] == hintervals_y[i][0]) {
++hncols;
}
int hnrows = (*count_intervals)[i] / hncols;
int ox = hintervals_y[i][0];
int oy = hintervals_x[i][0];
int nrows = hncols;
int ncols = hnrows;
int ci = 0;
int ri = 0;
int c = 0;
for (ri=0; ri<nrows; ++ri) {
for (ci=0; ci<ncols; ++ci) {
(*intervals_x)[i][c] = ox + ci;
(*intervals_y)[i][c] = oy + ri;
++c;
}
}
}
}
else {
*intervals_x = NULL;
*intervals_y = NULL;
}
#if DBG_SUBTASK
if (interval > 0) {
dbg = 0;
for (; dbg<num_subtasks-1; ++dbg) {
printf(“After vertical dividing, \
the %dth interval’s extent is from %d to %d in x dir, and from %d to %d in y dir\n”,
dbg, (*intervals_x)[dbg][0], (*intervals_x)[dbg][(*count_intervals)[dbg]-1],
(*intervals_y)[dbg][0], (*intervals_y)[dbg][(*count_intervals)[dbg]-1]);
}
}
printf(“After vertical dividing, load balance value is %f\n”, *load_balance);
#endif
/* free buffers */
free(hdata);
free(hbuf);
return 1;
}
这里的实现就更加简单了,思路就是把要进行垂直划分的区域先“横过来”,然后调用“水平划分”,最后再“竖过来”。
对于,同一个矩形区域,是要进行“水平划分”,还是要“垂直划分”呢,需要做一个总结:
int
straight_divide(int **task_mask, int cols, int rows, int num_subtasks, int interval,
int *flag_values, float *flag_weights, int flag_num,
int ***subtasks_x, int ***subtasks_y, int ***intervals_x, int ***intervals_y,
int **count_subtasks, int **count_intervals,
float *load_balance)
{
float lb_h = 0.f;
/* horizontal ptrs */
int **sx_h = NULL;
int **sy_h = NULL;
int **ix_h = NULL;
int **iy_h = NULL;
int *cs_h = NULL;
int *ci_h = NULL;
float lb_v = 0.f;
/* vertical ptrs */
int **sx_v = NULL;
int **sy_v = NULL;
int **ix_v = NULL;
int **iy_v = NULL;
int *cs_v = NULL;
int *ci_v = NULL;
if (!horizontal_divide(task_mask, cols, rows, num_subtasks, interval,
flag_values, flag_weights, flag_num,
&sx_h, &sy_h, &ix_h, &iy_h,
&cs_h, &ci_h,
&lb_h)) {
fprintf(stderr, “Error: failed to do horizontal dividing.\n”);
exit(1);
}
if (!vertical_divide(task_mask, cols, rows, num_subtasks, interval,
flag_values, flag_weights, flag_num,
&sx_v, &sy_v, &ix_v, &iy_v,
&cs_v, &ci_v,
&lb_v)) {
fprintf(stderr, “Error: failed to do vertical dividing.\n”);
exit(1);
}
if (lb_h >= lb_v) {
*subtasks_x = sx_h;
*subtasks_y = sy_h;
*intervals_x = ix_h;
*intervals_y = iy_h;
*count_subtasks = cs_h;
*count_intervals = ci_h;
*load_balance = lb_h;
free(sx_v);
free(sy_v);
free(ix_v);
free(iy_v);
free(cs_v);
free(ci_v);
#if DBG_SUBTASK
printf(“Horizontal dividing is selected for straight dividing\n\
, and its load balance value is %f\n”, lb_h);
#endif
}
else {
*subtasks_x = sx_v;
*subtasks_y = sy_v;
*intervals_x = ix_v;
*intervals_y = iy_v;
*count_subtasks = cs_v;
*count_intervals = ci_v;
*load_balance = lb_v;
free(sx_h);
free(sy_h);
free(ix_h);
free(iy_h);
free(cs_h);
free(ci_h);
#if DBG_SUBTASK
printf(“Vertical dividing is selected for straight dividing\n\
, and its load balance value is %f\n”, lb_v);
#endif
}
return 1;
}
将其命名为“straight divide” 。
这两个划分显然太简单了,所以,我又想到一个”十字划分“:将矩形区域的中心点作为原点,然后在垂直和水平方向各划一条线,划分为4个区域,为了让这四个区域的“负载均衡” 达到最大,让”原点“移动有限次(比如100,500),移动的原则是:向负载值较大的方向移动,如果达到预期的负载均衡值或者达到移动次数上限就停止移动。
其实现如下:
/*
* Description:
* move one step just in x direction or y direction, not both
*
* Params:
* origin_x: col_index(0 based) of point located at the upper left corner
* of central intervalling area
* origin_y: row_index(0 based)
*
* Returns:
* the load balance value after moving
*
* Note:
* x0[ind], `ind’ distributes:
* 0 1
* 2 3
*
* origin_x/y, is like: (points means interval area)
* . . . .
* 0 . . . . 1
* ..y/x . . ….
* …. ….
* …. midd ….
* …. . . ….
* 2 . . . . 3
*/
float
crossed_divide_move_xy(int **task_mask, int cols, int rows, int interval,
int *flag_values, float *flag_weights, int flag_num,
int *origin_x, int *origin_y)
{
int i = 0;
int x0[4];
int y0[4];
int x1[4];
int y1[4];
crossed_divide_find_xy_from_origin(*origin_x, *origin_y,
cols, rows, interval, x0, y0, x1, y1);
float loads[4];
for (i=0; i<4; ++i) {
loads[i] = crossed_divide_load_value(task_mask, x0[i], y0[i], x1[i], y1[i],
flag_values, flag_weights, flag_num);
#if DBG_SUBTASK
printf(“Loads of %dth subtask is: %f, with x0-%d, \
y0-%d, x1-%d, y1-%d\n”, i, loads[i], x0[i], y0[i], x1[i], y1[i]);
#endif
}
float yerr = 0.f;
float xerr = 0.f;
/* firsly, determine in which direction to move */
yerr = loads[0] + loads[1] – (loads[2] + loads[3]);
xerr = loads[0] + loads[2] – (loads[1] + loads[3]);
#if MOVE_ONE_STEP
if (fabs(yerr) >= fabs(xerr)) {
if (yerr != 0) {
if (yerr > 0) {
*origin_y -= 1;
}
else {
*origin_y += 1;
}
}
}
else {
if (xerr != 0) {
if (xerr > 0) {
*origin_x -= 1;
}
else {
*origin_x += 1;
}
}
}
#else
if (yerr > 0) {
*origin_y -= 1;
}
else {
*origin_y += 1;
}
if (xerr > 0) {
*origin_x -= 1;
}
else {
*origin_x += 1;
}
#endif
return load_balance(loads, 4);
}
/*
* Params:
* threshold: the threshold above which the dividing is acceptable and stops
*
*/
int
crossed_divide(int **task_mask, int cols, int rows, int interval,
float threshold, int max_trials,
int *flag_values, float *flag_weights, int flag_num,
int ***subtasks_x, int ***subtasks_y, int **intervals_x, int **intervals_y,
int **count_subtasks, int *count_intervals, float *lb)
{
if (interval <= 0) {
intervals_x = NULL;
intervals_y = NULL;
}
int origin_x = cols/2 – interval/2;
int origin_y = rows/2 – interval/2;
int x0[4];
int y0[4];
int x1[4];
int y1[4];
float loads[4];
int i = 0; // times of trials
*subtasks_x = (int **)calloc(4, sizeof(int *));
*subtasks_y = (int **)calloc(4, sizeof(int *));
*intervals_x = (int *)calloc(5, sizeof(int));
*intervals_y = (int *)calloc(5, sizeof(int));
crossed_divide_find_xy_from_origin(origin_x, origin_y,
cols, rows, interval, x0, y0, x1, y1);
#if DBG_SUBTASK
printf(“Start dividing crossedly…\n”);
printf(“Origin origin_x: %d, origin_y: %d\n”, origin_x, origin_y);
#endif
for (i=0; i<4; ++i) {
loads[i] = crossed_divide_load_value(task_mask, x0[i], y0[i], x1[i], y1[i],
flag_values, flag_weights, flag_num);
#if DBG_SUBTASK
printf(“Loads of %dth subtask is: %f, with x0-%d, \
y0-%d, x1-%d, y1-%d\n”, i, loads[i], x0[i], y0[i], x1[i], y1[i]);
#endif
}
float balance = load_balance(loads, 4);
#if DBG_SUBTASK
printf(“Origin load balance is: %f\n”, balance);
#endif
float maxb = balance;
int ox = origin_x;
int oy = origin_y;
if (balance < threshold) {
for (; i<max_trials; i++) {
#if DBG_SUBTASK
printf(“Starting %dth trial…\n”, i);
#endif
balance = crossed_divide_move_xy(task_mask, cols, rows, interval,
flag_values, flag_weights, flag_num,
&ox, &oy);
#if DBG_SUBTASK
printf(“At %dth trial, load balance value is %f\n”, i, balance);
#endif
if (balance > maxb) {
maxb = balance;
crossed_divide_find_xy_from_origin(ox, oy,
cols, rows, interval, x0, y0, x1, y1);
#if DBG_SUBTASK
printf(“After %dth trial, max load balance value changed to %f\n”, i, maxb);
#endif
if (maxb >= threshold) {
break;
}
}
}
#if DBG_SUBTASK
printf(“After %d times searches, the load balance %f is attained\n”,
i, maxb);
printf(“, with origin_x – %d, origin_y – %d\n”, ox, oy);
#endif
}
int j = 0;
for (; j<4; j++) {
(*subtasks_x)[j] = (int *)calloc((y1[j]-y0[j]+1)*(x1[j]-x0[j]+1), sizeof(int));
(*subtasks_y)[j] = (int *)calloc((y1[j]-y0[j]+1)*(x1[j]-x0[j]+1), sizeof(int));
}
*intervals_x = (int *)calloc(interval*(cols+rows-interval), sizeof(int));
*intervals_y = (int *)calloc(interval*(cols+rows-interval), sizeof(int));
int count = 0;
int k = 0;
for (j=0; j<interval; ++j) {
for (k=0; k<cols; ++k) {
(*intervals_x)[count] = k;
(*intervals_y)[count] = j + y1[0] + 1;
++count;
}
}
for (j=0; j<interval; ++j) {
for (k=0; k<rows; ++k) {
if (k >= y1[0]+1 && k <= y0[2]-1) {
continue;
}
(*intervals_x)[count] = j + x1[0] + 1;
(*intervals_y)[count] = k;
++count;
}
}
*count_intervals = count;
*count_subtasks = (int *)calloc(4, sizeof(int));
int m = 0;
for (; m<4; ++m) {
count = 0;
for (j=y0[m]; j<=y1[m]; ++j) {
for (k=x0[m]; k<=x1[m]; ++k) {
(*subtasks_x)[m][count] = k;
(*subtasks_y)[m][count] = j;
++count;
}
}
(*count_subtasks)[m] = count;
}
*lb = maxb;
return i;
}
* inervals’s dims should be 1, so count_intervals is just an integer, not an array
shelf_divide(int **task_mask, int cols, int rows, int num_subtasks, int interval,
while (sy[k/subns[i-1]][k%subns[i-1]][tnx] == sy[k/subns[i-1]][k%subns[i-1]][0]) {
printf(“For %dth task, ox- %d, oy- %d, ex- %d, ey- %d, nc- %d, nr- %d, offset- %d\n”,
while (sy[k/subns[nd-1]][k%subns[nd-1]][tnx] == sy[k/subns[nd-1]][k%subns[nd-1]][0]) {
printf(“For %dth task, ox- %d, oy- %d, ex- %d, ey- %d, nc- %d, nr- %d, offset- %d\n”,
printf(“After shelf-like dividing, load balance value is: %f\n”, *load_balance_value);
当然了,这只是在我所研究的区域这个特定条件下的结果,在其他应用条件下,结果显然会是不同的,其判定结果当然应该是在做了多次比较之后才能下结论的,但是无论如何,这几个划分对于水文模型的子任务分解都是有一定意义的。
不过凡事都有两面性:表面上看起来,“书架式划分”的负载均衡似乎提高了,但是,有两点却是损失了,其一,水平划分比较符合数据在主存中的排列顺序,可以有效减少cache miss,而垂直划分会增加程序对cahce line的需求从而增加cache miss的次数,最终也会对执行效率产生一定影响,当然了,如果数据量不大,影响也就很小了。其二,水平或垂直划分后的”隔离带“易于再次实施并行计算(核数-1),而书架式划分之后剩下的“隔离带”则相对复杂一点。
 ),迫切希望提高模型的执行速度的话,那么文中提到的方法以及代码也许会对你有些帮助。
),迫切希望提高模型的执行速度的话,那么文中提到的方法以及代码也许会对你有些帮助。 ,即便是考虑到线程切换的额外消耗,这个对比也太异常了一点。
,即便是考虑到线程切换的额外消耗,这个对比也太异常了一点。